#74 · La méprise du programme économique de la NUPES

Chère abonnée, cher abonné,

Twitter nous a gratifié hier l'une de ces pseudopolémiques dont les économistes de plateau télé ont le secret : Adrien Quatennens, député LFI, a déclaré que les 250 milliards d'euros que le programme de la NUPES avait prévu d'injecter dans l'économie génèreraient… 267 milliards d'euros de recettes fiscales. Et donc, ces 250 milliards de dépenses publiques se financeraient par eux-mêmes. Comme on le verra plus loin, ça n'est en réalité pas ce que dit le programme de la NUPES.

Cette déclaration de Quatennens, et les questions à mon avis légitimes qu'elle a provoquées, a été l'occasion pour que certains économistes de plateau télé se ruent sur leur générateur à fadaises. D'après l'un d'eux, sympathisant de la NUPES, un tel montant de recettes fiscales serait possible grâce à un effet bien connu en macroéconomie : l'effet multiplicateur.

Le principe de cet effet est simple : lorsque l'État dépense 1€, cet euro va créer de la richesse supplémentaire, qui va elle-même créer de la richesse supplémentaire, et ainsi de suite. Si l'effet multiplicateur est de 1.5 et que l'État dépense 10 milliards d'euros, ces 10 milliards d'euros créeront 10 × 1.5 = 15 milliards de richesses supplémentaires. Mesurer la valeur de l'effet multiplicateur est une question empirique — et on verra plus loin avec deux méta-analyses que les économistes ont de nombreuses mesures à leur disposition.

Reste que, et c'est vu en première année de macroéconomie à l'université, l'effet multiplicateur permet de prédire non pas le montant des recettes fiscales générées par une dépense publique, mais le montant de richesses crées par cette même dépense publique. Ce qui, à l'évidence, n'est pas du tout la même chose. Ce qui, en creux, pose la question suivante : quelle valeur le multiplicateur devrait-il avoir pour qu'une dépense publique de 250 milliards d'euros génère une recette fiscale de 267 milliards d'euros ? Et cette valeur du multiplicateur est-elle réaliste ?

Avant d'entamer le calcul (spoiler : son résultat ne plaira sans doute pas à certains de nos économistes de plateau télé), deux précisions. D'une part, je n'analyse pas le programme de la NUPES. Je m'intéresse uniquement à la méthode avec laquelle raisonnent certains de ces économistes de plateau télé. D'autre part, contrairement à ce que dit Quatennens, le programme de la NUPES ne prévoit pas 267 milliards de nouvelles recettes fiscales issues de l'effet multiplicateur. Comme le montre le screenshot ci-dessous, le programme prévoit "seulement" 35 + 27 = 62 milliards de nouvelles recettes fiscales issues de l'effet multiplicateur, le reste (267 - 62 = 205 milliards) étant levé grâce à ce qu'ils appellent une "révolution fiscale" — ce qui, je suppose, correspond à une refonte de la politique fiscale, et probablement à de nouveaux impôts.

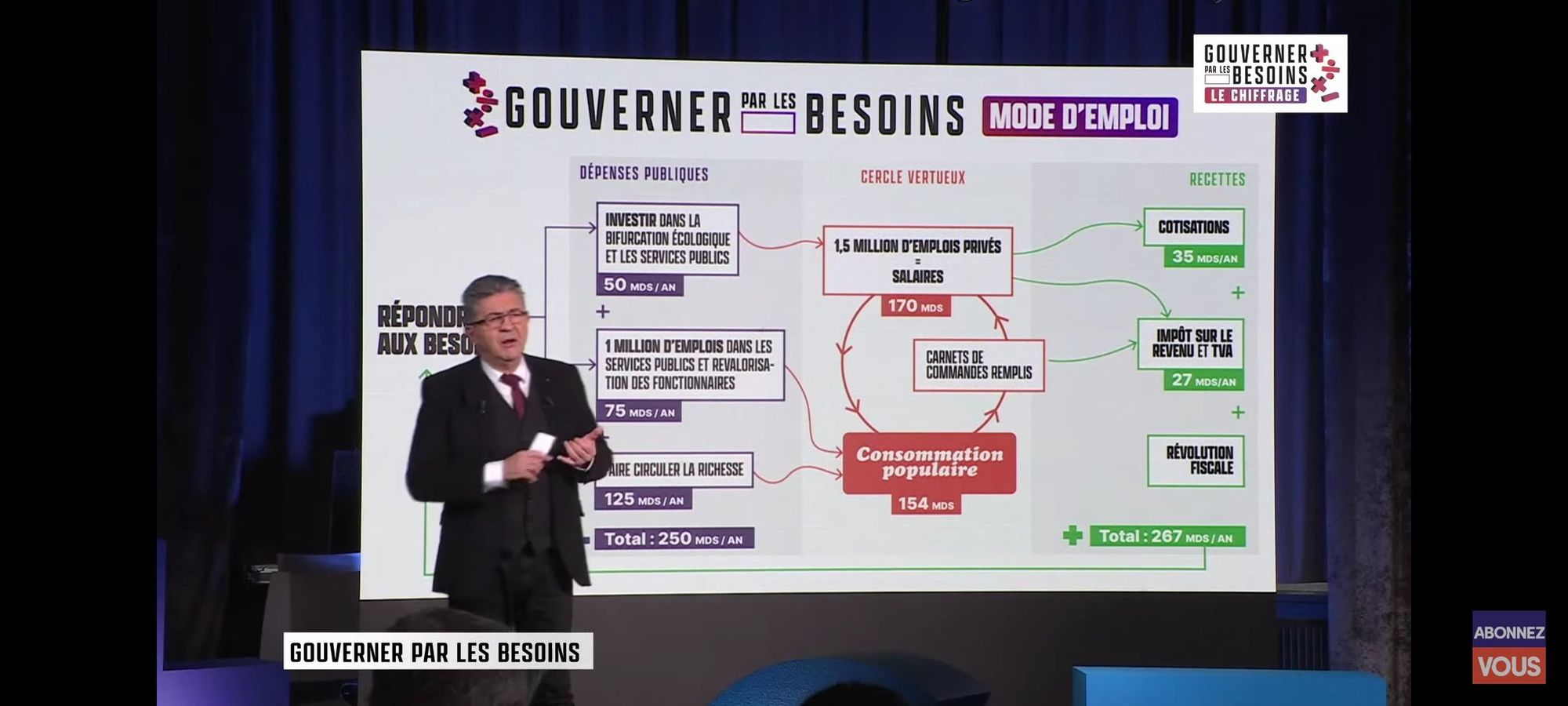
Parce que l'argument de Quatennens ne correspond pas au programme de la NUPES, il n'est pas possible de déduire quoi que ce soit sur le programme de la NUPES à partir des calculs qui vont suivre. Ou alors, ça serait commettre un bien vilain homme de paille.

Passons maintenant au calcul. Pour rappel, je cherche la valeur du multiplicateur qui permettrait à une dépense publique de 250 milliards d'euros de créer 267 milliards d'euros de recettes fiscales. Pour simplifier le calcul, je fais les hypothèses suivantes :

• l'économie est fermée, c'est-à-dire qu'il n'y a ni imports, ni exports
• il n'y a pas de contraintes sur l'offre, c'est-à-dire que la production peut augmenter à l'infini
• la dépense publique a des effets uniformes (= identiques) dans tous les secteurs d'activité de l'économie
• il n'y a aucun autre effet, par exemple d'éviction ou d'aubaine

Vous en avez peut-être déjà l'intuition, du fait de ces hypothèses le multiplicateur que je vais calculer est celui d'une économie très simplifiée — un peu comme si on calculait la vitesse de la chute d'une plume sur Terre sans prendre en compte l'effet de l'atmosphère.

De manière générale, le calcul qu'il faut poser est le suivant :

recette fiscale de l'injection = somme injectée × effet multiplicateur × taux de prélèvement obligatoire

Dans le cas qui nous occupe, nous avons :

267 = 250 × m × t

avec m l'effet multiplicateur et t ∈ [0,1] le taux de prélèvement obligatoire. Le taux de prélèvement obligatoire est la proportion de la richesse produite que l'État prélève via les taxes, les impôts et les cotisations. Ce que l'on cherche ici, c'est la valeur de m.

On connaît la valeur de t : en 2021, le taux de prélèvement obligatoire en France était de 44,3% du PIB, soit t = 0.443. On en déduit facilement la valeur de m :

267 = 250 × m × 0.443

⇔ 267 = m × 110.75

⇔ m = 267/110.75

⇔ m ≈ 2.41

Dans l’économie très simplifiée décrite plus haut, il faudrait que le multiplicateur ait une valeur d’au moins 2.41 pour qu’une dépense publique de 250 milliards d’euros génère une recette fiscale de 267 milliards d'euros.

En réalité, la valeur que le multiplicateur doit prendre pour générer 267 milliards de recettes fiscales peut être encore plus élevée. En 2018, environ la moitié des prélèvements obligatoires sont des cotisations sociales — c'est-à-dire le financement de la sécurité sociale, des retraites, etc. Les cotisations sociales n'étant pas directement contrôlées par l'État, il s'agit d'un type d'impôts un peu particulier. Selon que l'on intègre ou non les cotisations sociales dans le taux de prélèvement obligatoire, la valeur de m sera plus ou moins grande. Ci-dessous, j'ai calculé la valeur que devrait prendre le multiplicateur pour différents scénarios :

Selon le scénario que l’on retient, le multiplicateur doit avoir une valeur au moins supérieur à 2.41, parfois nettement plus, pour qu’une dépense publique de 250 milliards d’euros génère une recette fiscale de 267 milliards d’euros.

Avant de chercher à savoir si un multiplicateur égal ou supérieur à 2.41 est réaliste, j'aimerais discuter des limites de mon calcul.

• L’économie est fermée : en réalité, l’économie française est ouverte (elle commerce avec d’autres économies). Dans une économie ouverte, il faut que le multiplicateur ait une valeur plus élevée pour générer un même montant de richesses car une partie de la dépense publique créée de la richesse à l’étranger. Les valeurs du multiplicateur que je trouve sont donc des minimums.
• la dépense publique a un effet de même magnitude dans tous les secteurs de l’économie : en réalité, tous les secteurs d’activité ne bénéficieront pas des effets de la dépense publique de la même façon. Et chaque secteur d’activité, pour diverses raisons qui seraient trop longues à expliquer, peut avoir des taux de prélèvement obligatoire plus ou moins élevés par rapport au taux moyen. Il faudrait donc, pour être précis, calculer l’effet de la dépense publique non pas directement au niveau agrégé comme je le fais, mais secteur par secteur et faire ensuite la somme de l'effet sur tous les secteurs.
• il n'y a aucun autre effet : l'économie est un système dynamique. En langage d'économistes, il y a des effets dits endogènes, c'est-à-dire des effets économiques causés par des causes internes à l'économie. Il faudrait prendre en compte tout ou partie ces effets pour avoir une valeur plus réaliste de m.

Pour toutes ces raisons, il faut prendre cette valeur de m = 2.41 comme un strict minimum. La véritable valeur que devrait prendre mpour qu'une dépense publique de 250 milliards d'euros génère une recette fiscale de 267 milliards d'euros est très vraisemblablement supérieure.

Venons-en maintenant à savoir si un multiplicateur avec une valeur égale ou supérieure à 2.41 est réaliste. Une fois encore, la valeur du multiplicateur est une question empirique. D'après cette méta-analyse de mai 2022, actuellement au stade de working paper (donc pas encore revue par les pairs), la réponse est plutôt non.

Cette méta-analyse synthétise les résultats de 132 articles de recherche, qui correspondent à 3200 observations. Comme on le voit sur le graphique ci-dessous qui montre les mesures réalisées dans les différents articles, un multiplicateur dont la valeur est supérieure à 2.41 (à droite de la ligne bleue) est relativement peu fréquemment observé.

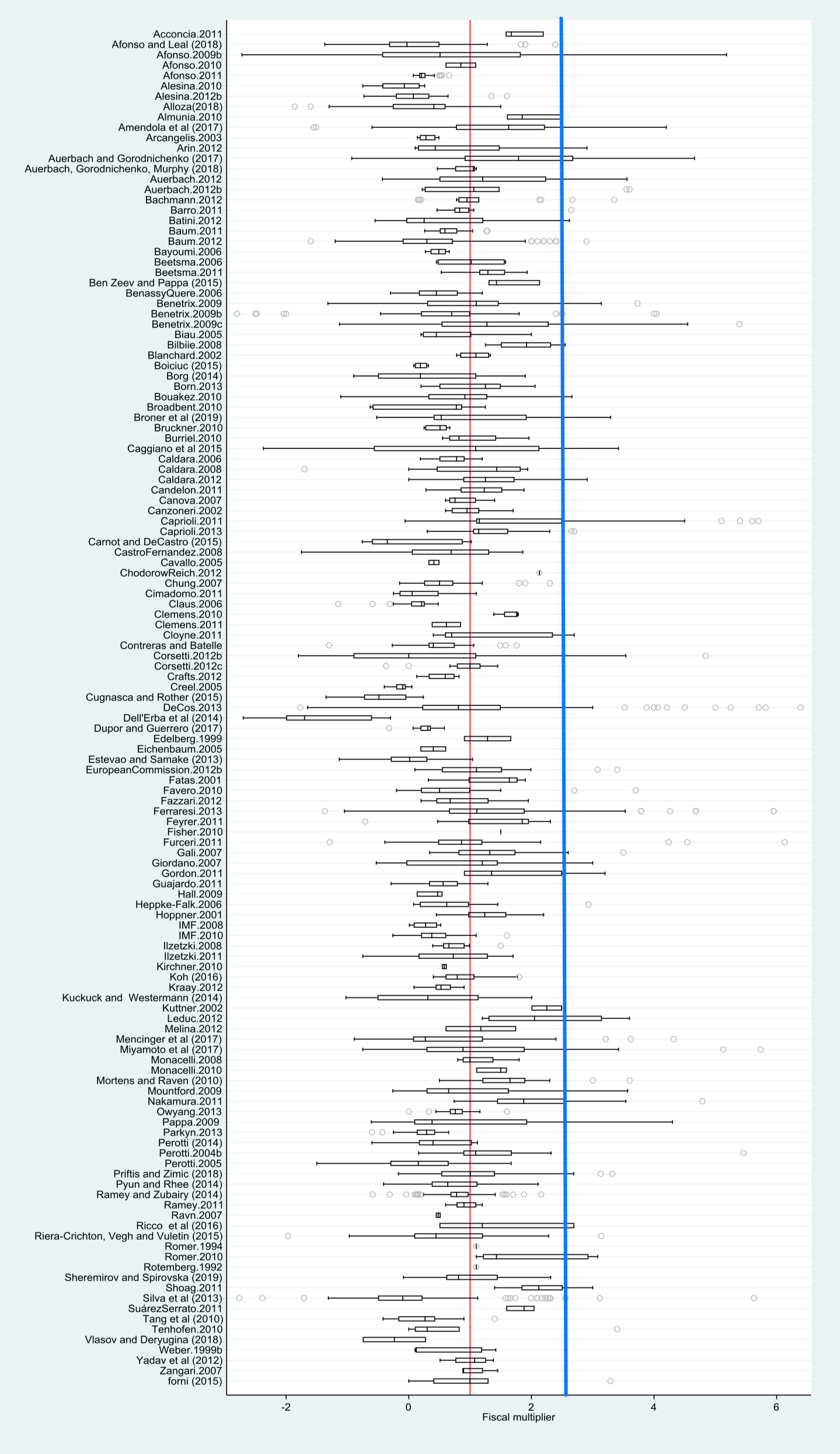
Si l'on décompose les résultats par pays, on se rend compte qu'un multiplicateur de 2.41 pour la France est peu probable :

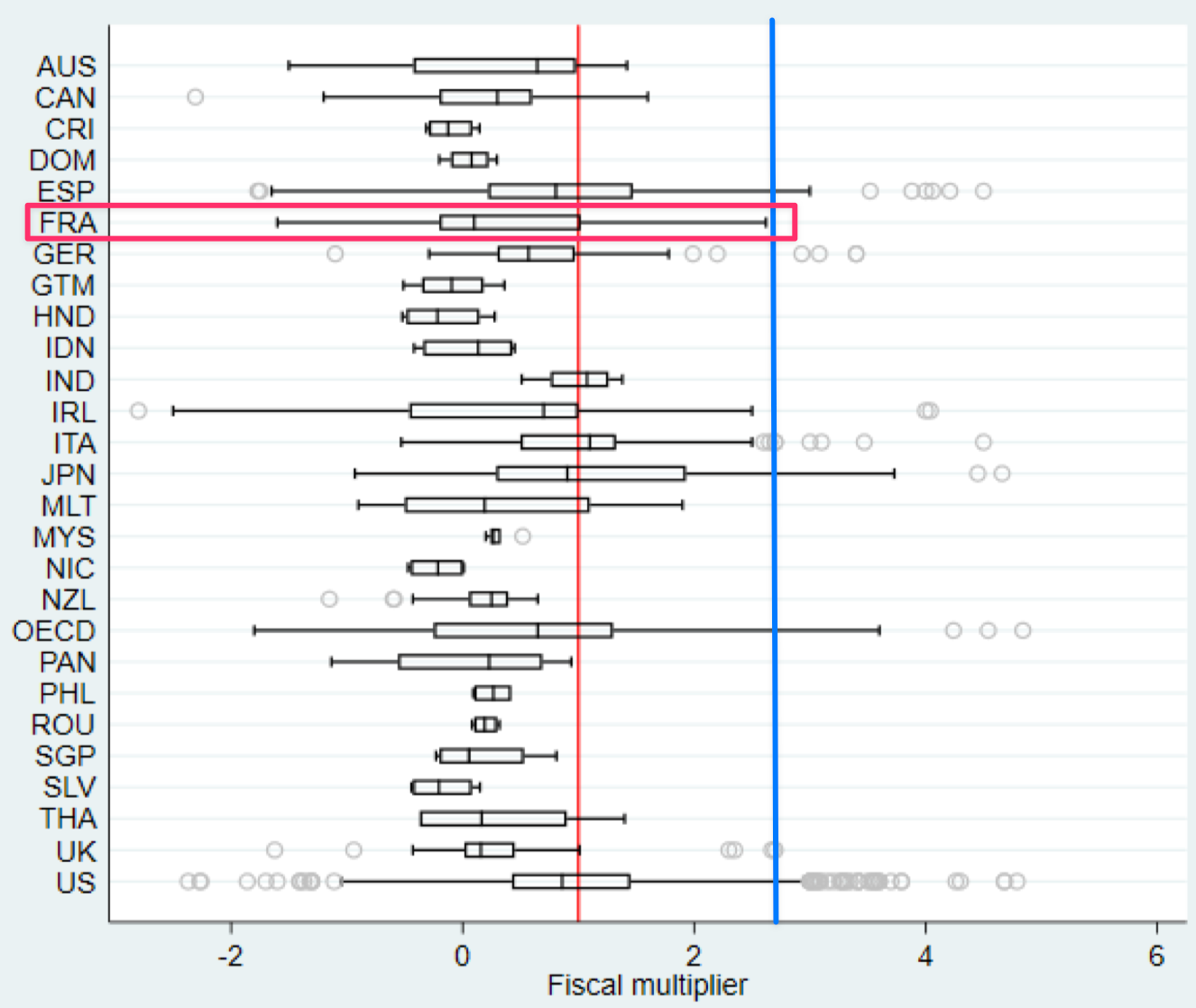
Pour autant, la valeur du multiplicateur varie vraisemblablement dans le temps. Une autre méta-analyse, publiée en 2018 dans le Journal of Economic Surveys, montre que la valeur du multiplicateur peut augmenter de 0.7 à 0.9 point lorsque l'économie traverse une période difficile. Dans l'absolu et sous les bonnes conditions, on peut sans doute se convaincre qu'il est donc possible que le multiplicateur en France prenne une valeur égale ou supérieure à 2.41. Mais attention : ça n'est pas parce que c'est possible que c'est effectivement le cas. Encore une fois, il s'agit d'une question empirique : seules les données permettront de trancher.

De manière générale, il me semble relativement clair qu'un multiplicateur dont la valeur est égale ou supérieure à 2.41, pour la France, est peu probable. En d'autres termes : qu'une dépense publique de 250 milliards d'euros génère 267 milliards d'euros de recettes fiscales est peu probable.

Faut-il conclure que le programme de la NUPES n'est pas réaliste ? À partir de ce que j'écris ici, il est impossible de répondre ni dans un sens, ni dans l'autre, à cette question. Comme je l'écrivais plus haut, ce numéro n'est pas une analyse du programme de la NUPES. D'autant, je le répète, que le programme de la NUPES ne prévoit pas267 milliards d'euros de recettes fiscales liées à l'effet multiplicateur. Les 62 milliards que le programme prévoit nécessitent (dans le même cadre simplifié de mon calcul) un multiplicateur d'au moins 0.56 — une valeur beaucoup plus réaliste.

Ce que je dis, par contre, c'est que les économistes de plateau télé qui, dans le cas présent, se donnent en spectacle sur Twitter, ont recours à une méthode de raisonnement dont la robustesse m'interroge. Je ne suis pas macroéconomiste, pourtant il m'a tout de suite semblé douteux qu'une dépense publique de 250 milliards d'euros puisse générer 267 milliards d'euros de recettes fiscales ; comme on l'a vu plus haut, un tel montant de recettes fiscales nécessiterait un multiplicateur dont la valeur est bien improbable. Et pour avoir moi enseigné la macroéconomie en première année à la faculté d'économie de Nancy, sans même avoir fait les calculs il était clair que le multiplicateur requis pour atteindre un tel montant de recettes fiscales était irréaliste.

Le problème, me semble-t-il, est que ces économistes de plateau préfèrent faire le show plutôt qu'expliquer, éclairer ou alimenter le débat avec des arguments de fond. C'est probablement moins sexyque de clasher, de manière totalement fallacieuse soit dit en passant, l'ancien économiste en chef du FMI.

Et peu importe si à la fin, c'est contreproductif. Car défendre l'argument qu'une dépense publique de 250 milliards d'euros puisse générer 267 milliards d'euros de recettes est bel et bien contreproductif. D'une part, clasher plutôt qu'expliquer n'informe personne — au point que Porcher s'emmêle lui-même les pinceaux dans sa définition de l'effet multiplicateur, tirant au passage une évitable balle dans le pied de sa crédibilité. D'autre part et surtout, le programme de la NUPES ne prévoit encore une fois pas 267 milliards de recettes fiscales générées par l'effet multiplicateur ! Porcher défend, avec des attaques personnelles, des arguments fallacieux et des définitions de niveau première année fausses, une proposition qui n'existe tout simplement pas. On atteint là le sommet, me semble-t-il, du contreproductif. Il aurait sans doute été plus efficace de corriger les propos de Quatennens avec la véritable proposition du programme de la NUPES.

Mais non, à la place il a fallu se jeter à la gorge des personnes qui, à juste titre, ont remis en question le propos de Quatennens. Cela dénote bien, de mon point de vue, l'extrême fragilité de la méthode utilisée par les économistes de plateau télé. Et, en creux, du niveau de confiance à accorder à leurs propos.

L'Économiste Sceptique est intégralement financé par vous, ses abonnées et abonnés. Si vous aimez mon travail, vous pouvez me rémunérer en me soutenant financièrement et accéder à l'intégralité de mon contenu en devenant membre Plus. Vous recevrez un deuxième numéro par semaine et une fois par mois, vous pourrez participer à une visioconférence privée avec moi et les autres membres Plus. Aux abonnées et abonnés qui sont déjà membres Plus, merci à vous !

À bientôt pour le prochain numéro de L'Économiste Sceptique,
Olivier